Distributed Pursuit-Evasion Game of Limited Perception USV Swarm Based on Multiagent Proximal Policy Optimization
方法概要
该文章提出一种用于多USV的追逃博弈的分布式捕获策略优化方法,基于MAPPO算法,结合速度控制机制,形成动态包围圈;网络层采用Bi-GRU;策略方面采用动态障碍物(速度和方向)和课程学习技术。
状态表示
追捕者的局部观测由三部分组成,分别为:1. 自身状态,包括:当前速度,通过速度控制机制计算出的期望速度,碰撞半径和航向;2. 感知范围内第1到第m个相邻追捕者,分别包括:与第n个相邻者生成的VO区域,欧氏距离以及$\frac{1}{t_n}$ ($t_n$为预测的碰撞时间);3. 感知范围内第1到第q个静态障碍物,分别包括与第p个相邻者生成的VO区域,欧氏距离以及$\frac{1}{t_p}$ ($t_p$为预测的碰撞时间)。
对于2,3组成部分,按欧氏距离对其进行排序,并裁剪为一个固定维度的向量,即限制数量,最终以一个128维固定长度的向量输入到Bi-GRU网络中。
对于不同的追捕者的观测状态排序问题,基于相对角度$\alpha_r$重新组织观测状态,其表示追捕者和逃避者速度方向之间的角度。
奖励函数设计
$$r_i = r_{vo} + r_{col} + r_{f}$$
其中,$r_{vo}$是一个即时奖励,用于鼓励追捕者尽可能选择VO区域之外的速度,以避免在追捕过程中遇到障碍
$$ r_{vo} = \begin{cases} l_1 - l_2 \cdot \left | \mathrm{v} - \mathrm{v^{des}} \right | , \quad \mathrm{v} \notin \mathrm{VO} \quad or \quad t > t_s \\ l_3 - L_4 \cdot (t + 0.1)^{-1}, \quad \mathrm{v} \in \mathrm{VO} \quad and \quad t > 0.1 \cdot t_s \\ -l_5 \cdot (t + 0.1)^{-1}, \quad t < 0.1 \cdot t_s \end{cases} $$
其中$\mathrm{v}$和$\mathrm{v^{des}}$分别表示追逐者当前速度和速度控制机制输出的期望速度,$l_1$ 和 $l_2$ 是用于鼓励追逐者接近逃避者的可调参数,$t$ 是估计的碰撞时间,$t_s$ 是安全避障时间。当追逐者的速度在 VO 区域内时,且小于$0.1 \cdot t_s$,$l_5$ 用于惩罚这种行为。当追逐者的速度在 VO 区域内时,应分配负奖励以惩罚这种行为,其中 $l_3$ 和 $l_4$ 表示奖励系数。向量 $C_{VO} = [\mathrm{v}_P, \mathrm{v}_l, \mathrm{v}_r ]^T$ 可用于确定当前速度 \mathrm{v} 是否在 VO 区域内。
$$ \begin{matrix} \mathrm{v} \notin VO : (\mathrm{v} - \mathrm{v}_p) \times\mathrm{v}_l < 0 \vee (\mathrm{v} - \mathrm{v}_p) \times\mathrm{v}_r > 0 \\ \mathrm{v} \in VO : (\mathrm{v} - \mathrm{v}_p) \times\mathrm{v}_l \ge 0 \vee (\mathrm{v} - \mathrm{v}_p) \times\mathrm{v}_r \le 0. \end{matrix} $$
当 $t < 0.1\cdot t_s$ 时,意味着追踪者即将在短时间内发生碰撞,应给予负奖励。
$r_{col}$ 是一种延迟奖励,当发生碰撞时提供负奖励。通过整合即时奖励和延迟奖励,它允许追逐者同时考虑当前任务和长期目标。
$r_f$ 是对包围阵型的奖励,旨在激励追捕者均匀地分布在逃避者周围,定义如下:
$$r_f = -l_6 \cdot \frac{1}{n} \sum_{i=1}^n d_{1E} \cdot d_{iE}$$
其中$\hat{d}_\mathrm{iE}$是从追逐者$i$指向逃避者的单位向量,$r_f$的范围是$[−l_6, 0]$,并且更高的值表示更好的包围队形,应该注意的是,只有当$n \ge 2$时,队形奖励$r_f$才有意义。
算法架构图
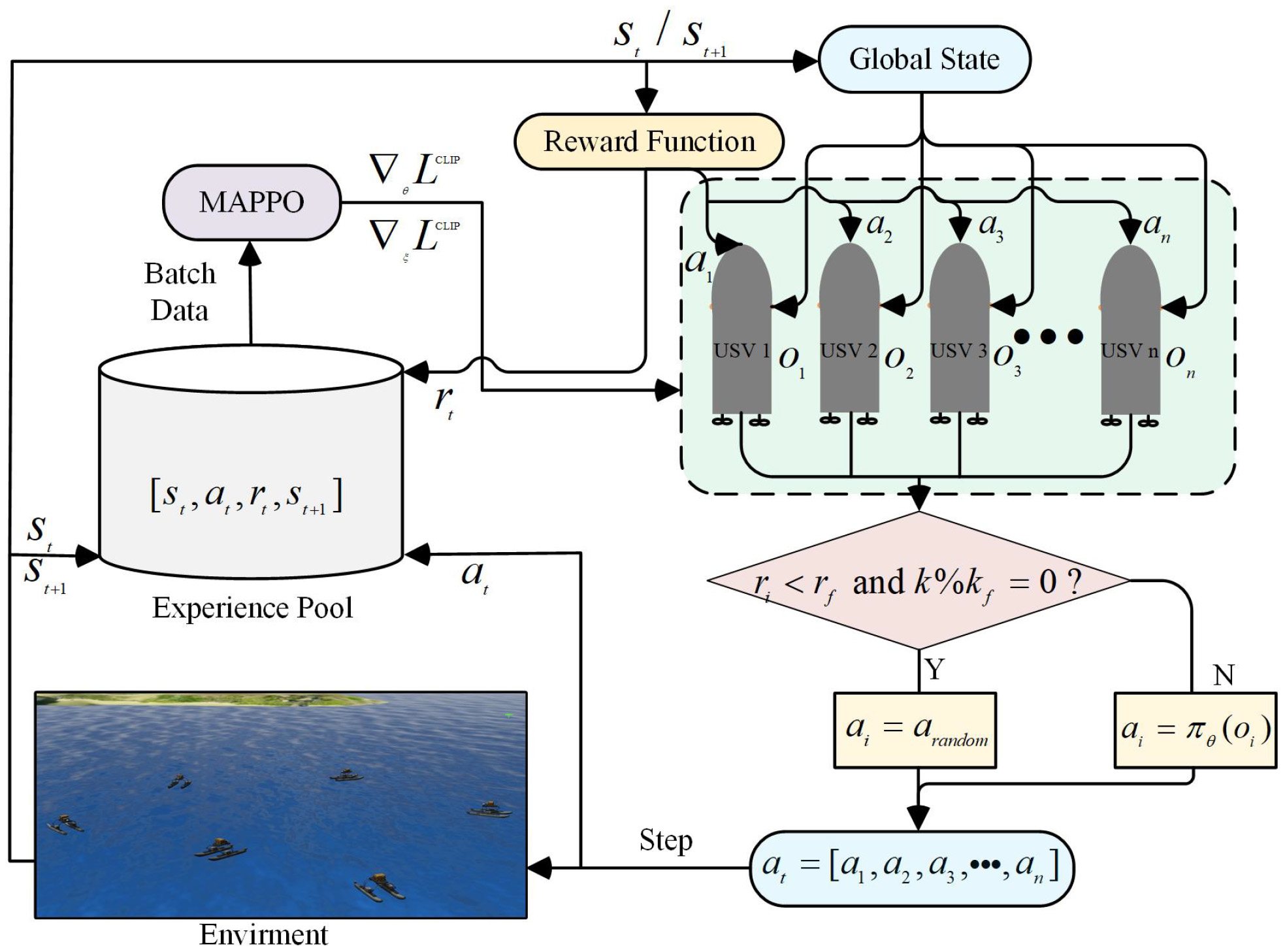
由于MAPPO采用随机策略,其策略网络输出动作为概率分布。为了增强MAPPO的随机探索能力,引入了虚拟障碍,并设置其为随机动作选择,有利于更好地处理不确定性,加速训练收敛,并提高策略的泛化能力。
课程学习
多无人艇追逃场景通常包含多个追逐者和逃避者。直接针对大规模捕获任务进行训练通常会导致策略收敛缓慢和奖励稀疏问题。此外,追逐者和逃避者的相对速度以及包围半径也会影响捕获任务的难度。
因此,将课程学习融入到训练过程中,该过程从一个小规模的捕获任务、一个较大的包围半径和较慢的移动速度开始进行训练。这种方法鼓励追捕者在初始阶段探索复杂的捕获行为。随后,通过调整无人艇群的大小、包围半径和无人艇的速度,逐渐增加捕获任务的难度,直到与实际难度相符。
课程学习提供了一种渐进式的训练策略,使追逐者能够更有效地学习,并应对最初难以获得积极奖励的情况。这种训练技术通过探索引导和任务排序,有效地解决了稀疏奖励问题,并增强了追逐者在解决复杂捕获任务中的鲁棒性。
课程学习过程:首先使用三艘USV(一艘逃避者和两艘追逐者)在无障碍场景中进行训练;然后向场景中添加障碍物;最后逐渐增加追逐者的数量到四艘。逃避者的最大速度设置为追逐者最大速度的80%
超参数设置
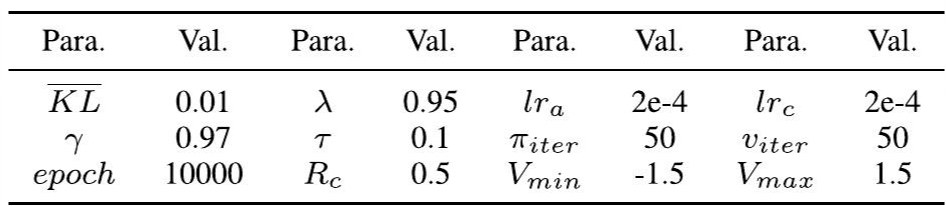
结论
本文研究了多无人水面艇(USV)追逃博弈问题,并提出了一种适用于具有有限感知范围的USV集群的分布式捕获控制方法。所提出的方法是一种端到端的控制方法,不需要系统模型的知识。该方法具有在未知环境中自主学习和持续优化捕获策略的能力。通过增强传统的MAPPO训练框架,并在训练过程中加入课程学习,该方法进一步提高了策略的探索性能和收敛速度。通过对比仿真实验和虚拟现实场景测试,验证了该方法的有效性。实验结果表明,该方法在策略收敛速度、捕获效率和泛化能力方面具有显著优势,并在实际场景中具有潜在的适用性。未来的研究将侧重于探索涉及多个追逐者和多个逃避者的追逃博弈问题,以及策略从仿真到实践的转移。
- Li F, Yin M, Wang T, et al. Distributed pursuit-evasion game of limited perception USV swarm based on multiagent proximal policy optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2024.



