Multi-USV cooperative encirclement strategy based on the double-layer prioritized replay mechanism in the reef sea area
概述
本文在MADDPG算法的基础上，增加了自监督辅助任务和双层优先级重放机制，实现了复杂礁石海域中多艘USV的集体包围和捕获。主要贡献为：
- 提出了一种融合行为优化、角度约束和安全保护的多维奖励机制，以确保导航安全并提高包围和捕获成功率；
- 双层优先级经验回放：使用全局优先级（基于TD误差）和局部优先级（基于回合进度和状态值）来反映智能体预测误差的程度，并在关键时刻提高学习效率。使用重要性采样权重来纠正采样偏差，以确保无偏估计；
- 自监督辅助任务：通过预测环境中的内部结构和隐藏信息，有助于智能体更好地理解环境动态，从而提高主要任务的学习效率和最终性能。在复杂合作场景（如多智能体包围和捕获）中，它不仅提高了学习效率，还增强了智能体对环境动态和合作模式的理解。
双层优先经验回放
双层优先经验回放引入了两个层次的优先级评估机制。第一层是全局优先级维度，主要基于误差评估样本的学习价值，反映了样本对价值函数近似误差的贡献。当智能体的预测与实际回报之间存在较大差异时，表明该样本包含重要的学习信息。在包围任务中，意味着具有意外情况或关键决策点的经验将被分配更高的全局优先级。全局优先级的核心公式： $$ TD_{error}^i = |r + \gamma \cdot Q_target(s’, \mu’(s)) - Q(s,a)| \\ P_{global}^i = (|TD_error_i| + \epsilon)^\alpha $$
其中：$TD_{error}^i$是样本$i$的时序差分误差，$\epsilon > 0$是一个小的常数，用于防止优先级为0，$\alpha \in [0,1]$控制优先级分布的锐度。当$\alpha$接近0时，所有样本的抽样概率趋于均匀，退化为传统方法；当$\alpha$接近1时，优先级差异被最大程度地放大。
第二个层次，即局部优先级难度，考虑了特定于任务的重要性因素。在多USV包围场景中，这包括几个关键方面：首先，早期的探索行为和包围圈的最后阶段都具有特殊价值；其次，在接近成功包围时的关键时刻做出的决定直接影响任务的失败；最后，回合结束时是成功或者失败，都包含完整策略执行的结果信息。局部优先级方程： $$ P_{global}^i = \beta_1 \cdot f_{capture}(d) + \beta_2 \cdot f_{episode}(b) + \beta_3 \cdot f_{coordination}© $$
其中$f_{capture}(d_i)=exp(-d_i/\sigma)$表示捕获距离因子。使用指数衰减函数，这意味着更接近成功捕获的经验会被赋予更高的优先级。$f_{episode} = max(0, (t-150) / 200)$表示回合进度因子，反映了对时间维度重要性的考虑。这种分段函数设计更符合捕获任务的实际特征。在早期阶段，主要涉及接近和定位，只有在后期阶段才会进行实际捕获。$f_{coordination}(c_i)$表示多USV协调质量因子。$\beta_1, \beta_2,\beta_3$是权重参数。符合优先级结合了上述两层信息：
$$ P_{combined}^i=(P_{global}^i)^\lambda \cdot (P_{local}^i)^{(1 - \lambda)} $$ 在早期阶段，可能更多地依赖于TD误差，而在后期阶段，则更多地依赖于特定于任务的信息，最终采样概率： $$ P_{sampling}^i = \frac{P_{combined}^i}{\sum_j P_{combined}^j} $$ 为了确保估计的无偏性，引入重要性采样权重： $$ \omega^i = (N \cdot P_{sampling}^i)^{-\beta} \\ \hat W_i = \frac{\omega^i}{max_j(\omega^j)} $$
参数$\beta$控制偏差校正的强度。当$\beta = 0$时，不进行校正；当$\beta = 1$时，偏差被完全校正。在实际应用中，$\beta$通常从一个较小的值逐渐增加到1。它允许在训练的初始阶段存在一定程度的偏差以加速学习，并在后期逐渐纠正它以确保收敛。
双层优先级机制发挥着关键作用。这种设计的核心优势在于它能够更准确地识别和利用对学习最有价值的经验。在诸如海上包围和捕获等复杂协调任务中，简单的TD误差可能无法完全捕捉到特定于任务的重要性。通过结合学习误差和任务语义，双层机制确保训练过程能够专注于具有最大学习价值的经验。
自监督辅助任务的数学模型
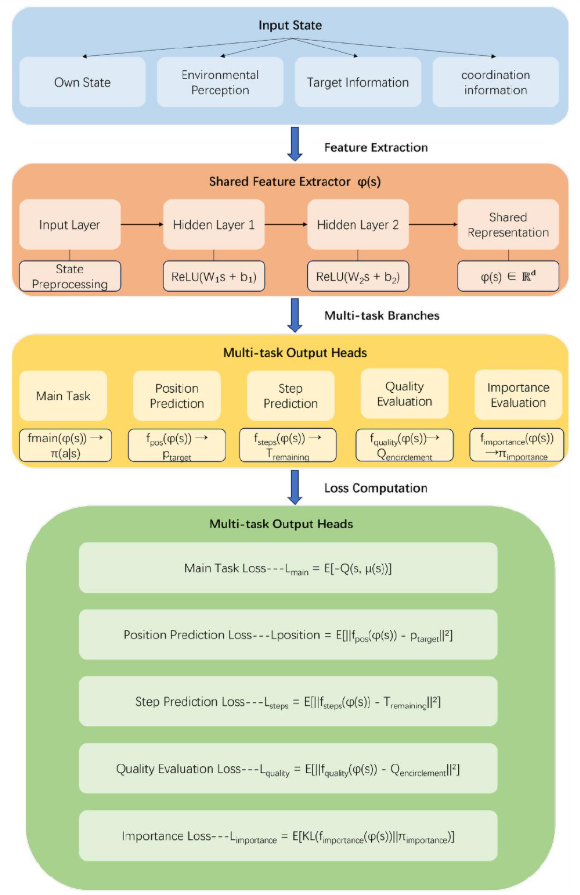
传统强化学习，神经网络通常只有一个用于预测Q值或策略的输出头。该文章引入自监督辅助任务，将单头输出改为多头输出并同时执行多个预测任务。总体目标函数由主要任务和辅助任务的加权组合组成，这反映了一种多维学习策略。网络架构如图所示：
总体目标函数体现了多任务学习的核心思想，即通过解决相关的辅助任务来提高主要任务的学习效果。总体目标函数为：
$$
L_{total} = L_{main} + \sum_k \lambda_k \cdot L_{aux_k}
$$
其中，$L_{main} = E[-(Q(s,\mu (s)))]$代表主要任务的策略梯度损失，$L_{aux_k}$表示第k个辅助任务的损失，$\lambda_k$代表第k个辅助任务的权重。这种加权组合的设计反映了相关任务之间存在共享特征，学习这些共享特征可以提高泛化能力。在包围任务中，诸如预测目标位置和评估包围质量等辅助任务都需要理解空间关系和动态变化，而这些能力直接有助于主要的包围决策任务。
在海域中，目标可能采取各种规避策略。通过预测其位置，包围智能体可以更好地理解目标的意图和可能的移动轨迹，从而指定更有效的包围策略。位置预测损失方程为： $$ L_{position} = \mathbb{E}[\left| f_{pos}(\varphi(s)) - p_{target} \right|^2] $$ 其中，$\varphi(s)$是共享特征提取器的输出，$f_{pos}$是位置预测头网络，$p_{target}$是目标USV的真实位置。
包围步骤预测任务培养了智能体的时间规划能力和对任务进度的感知。在实际海上行动中，准确估计包围时间对于资源分配和战略调整至关重要。这种预测能力有助于智能体在长期规划和短期执行之间找到平衡。步骤预测损失方程为： $$ L_{steps} = \mathbb{E}[\left| f_{steps}(\varphi(s)) - T_{remaining} \right|^2] $$ 其中，$f_{steps}$是步数预测头网络，$T_{remaining}$是包围剩余步数的估计值。
包围质量评估任务旨在评估当前包围阵型的有效性。质量评估损失方程为： $$ L_{quality} = \mathbb{E}[\left| f_{quality}(\varphi(s)) - Q_{encirclement} \right|^2] $$ 其中，$f_{quality}$是质量评估头网络，$Q_{encirclement}$是包围阵型的质量得分。
对于智能体重要性预测任务，KL散度衡量两个概率分布之间的差异。它不是对称的，并且我们更关心预测分布对真实分布的近似，而不是相反的情况。在协调任务中，这意味着网络学习识别哪些智能体在当前情况下起关键作用。重要性分布损失方程为： $$ L_{importance} = \mathbb{E}[KL（f_{importance}(\varphi(s)) \left| \pi_{importance} \right] $$ 其中，$f_{importance}$输出智能体重要性分布，$\pi_{importance}$是基于奖励计算的真实重要性分布，而KL是KL散度。
这两种机制的结合产生显著的协同效应。双层经验回放确保学习过程能够充分利用最有价值的经验，而自监督学习丰富了从每个经验中提取的信息量。在学习效率方面，自监督任务提供了更密集的学习信号。传统的强化学习只能从稀疏的任务奖励中学习，而辅助任务在每个时间步都提供有意义的监督信号。这尤其适用于长序列决策任务，例如海域包围，在这种任务中，成功的奖励信号可能要到包围完成才会出现。
在样本利用效率方面，双层优先级机制确保关键经验被重复学习，并且自监督任务从每个样本中提取更多信息。这种组合大大提高了学习过程的数据效率。在泛化能力方面，辅助任务帮助网络学习更通用的环境理解和协调技能。通过预测目标位置和评估包围质量，智能体能够深入理解环境动态和任务状态，并且这些技能可以转移到不同的海况和目标行为模式。在协调性能方面，智能体重要性评估任务能够促进更好的团队协调。当一些智能体由于设备故障或环境因素而无法正常工作时，系统可以自动重新分配任务。
